A paradox in high dimensional geometry

This “paradox” was explain to me by a colleague. Take a square whose side have length $1$ (on blue on the figure below) and subdivide it in four squares of side $1/2$.

In the middle of each smaller square place a disc which is tangent to the four sides (on white on the picture below). In particular the radius of these disc is $1/4$.

Now place a fifth disc (red on the picture below), centered at the center of the original (blue) square which is tangent to the four other discs.

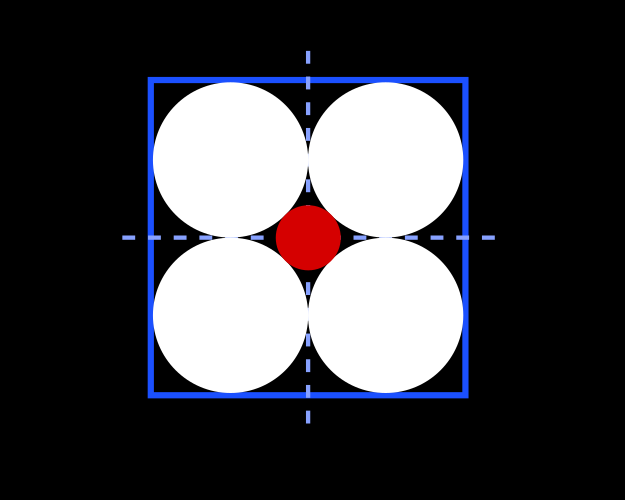
What is the radius $r_2$ of this small red disc? A computation using Pythagoran theorem shows that $$ r_2 = \frac {\sqrt 2}4 - \frac 14 \approx 0.104.$$

Now let’s do the same in dimension $3$: start with a (blue) cube of side $1$; subdivide it into $8$ small cubes of size $1/2$; in each small cube put a (white) ball of radius $1/4$; complete the picture with a small (red) ball at the center of the initial cube, which is tangent to the $8$ other balls. The radius of the later ball is now: $$ r_3 = \frac {\sqrt 3}4 - \frac 14 \approx 0.185.$$

There is no reason to stop in dimension $3$. We can do the same construction in dimension $4$, $5$, $6$,… How does the situation looks in arbitrary dimension $n$? We still have a (blue) hypercube of side $1$. It is subdivided into $2^n$ smaller cubes of side $1/2$, each of them contains a (white) ball of radius $1/4$. In the middle of the (blue) cube lies a small (red) ball of radius $$ r_n = \frac {\sqrt n}4 - \frac 14 .$$ A small ball ? Really ? As the dimension $n$ tends to infinity, the radius $r_n$ also tends to infinity. Which means that if $n$ is large enough (more precisely $n > 9$) then the red ball does not fit in the blue cube anymore!

How can we observe this phenomenon? The videos below show the intersection of the scene with a $4$ dimensional subspace. More precisely, if $\{\vec v_1, \vec v_2, \vec v_3, \vec v_4\}$ is an orthonormal family of vectors in $\mathbf R^n$, then the picture at time $t$ is the intersection of the figure with the $3$-dimensional affine subspace $$ A_t = t\vec v_4 + {\rm span}(\vec v_1,\vec v_2,\vec v_3).$$ The intersection of a $n$-dimensional ball with $A_t$ is still a ball. The intersection of the cube with $A_t$ is a convex polyhedron pictured by its $1$-skeleton

Simulations

For each simulation we provide a $4\times n$-matrix. Its $i$-th row represents the coordinates in $\mathbf R^n$ of a vector $\vec w_i$. The vectors $\{\vec v_1, \vec v_2, \vec v_3, \vec v_4\}$ defining the section are obtained from $\{\vec w_1, \vec w_2, \vec w_3, \vec w_4\}$ by the Gram-Schmidt orthonormalization algorithm.

Dimension 4

In dimension 4 the inner red ball still fits in the cube.

$$\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \newline 0 & 1 & 0 & 0 \newline 1 & 1 & 1 & 1 \newline 1 & 1 & 1 & -1 \end{array}\right)$$

$$\left(\begin{array}{cccc} 82 & 13 & 53 & 36 \newline 63 & 9 & 29 & 7 \newline 29 & 73 & 96 & 59 \newline 67 & 36 & 53 & 90 \end{array}\right)$$

Dimension 12

In dimension 12, if we choose the section carefully we observe the inner red ball escaping from the cube.

$$\left(\begin{array}{ccccccc} 1 & 0 & 0 & \cdots & 0 & 0 & 0 \newline 0 & 1 & 0 & \cdots & 0 & 0 & 0 \newline 1 & 1 & 1 & \cdots & 1 & 1 & 1 \newline 1 & 1 & 1 & \cdots & 1 & 1 & -1 \end{array}\right)$$

However if we use a random section, the phenomenon becomes invisible.

$$\left(\begin{array}{cccccccccccc} 54 & 47 & 4 & 74 & 38 & 53 & 7 & 73 & 90 & 20 & 30 & 58 \newline 38 & 87 & 25 & 28 & 44 & 59 & 63 & 15 & 65 & 20 & 37 & 11 \newline 53 & 88 & 81 & 86 & 20 & 4 & 42 & 47 & 95 & 58 & 15 & 4 \newline 65 & 37 & 18 & 56 & 20 & 62 & 49 & 82 & 18 & 66 & 93 & 72 \end{array}\right)$$

Dimension 20

The picture is even sharper in dimension 20.

$$\left(\begin{array}{ccccccc} 1 & 0 & 0 & \cdots & 0 & 0 & 0 \newline 0 & 1 & 0 & \cdots & 0 & 0 & 0 \newline 1 & 1 & 1 & \cdots & 1 & 1 & 1 \newline 1 & 1 & 1 & \cdots & 1 & 1 & -1 \end{array}\right)$$

Dimension 50

In dimension 50, even with a random section, we see the inner red ball escaping the cube. Nevertheless this section does not intersect any white ball.

$$\left(\begin{array}{c} \newline \text{A random $4\times 50$-matrix!} \newline
\newline
\end{array}\right)$$