Desargues meets Boy
The Desargues Theorem drawn on a Boy’s surface. Design: R. Coulon
Projective geometry is an important mathematical discovery that goes back to the work of Desargues in the XVIIth century.
The projective plane
The real projective plane is the space of lines in $\mathbb R^3$ going through the origin. Alternatively it can be obtained for the north hemisphere of the unit sphere in $\mathbb R^3$ by identifying opposite points on the equator. It contains as a subset the usual real plane but cannot be embedded in $\mathbb R^3$.
The Boy surface
The best we can hope for is an immersion of the real projective plane in $\mathbb R^3$. This is precisely what the Boy surface is. Invented by Werner Boy there are several parametrization of this surface. The one pictured below is attributed to F. Apery.
Another parametrization, due to Bryant and Kusner has the property to be the “least bend” immersion of the Boy surface. Below a bronze model built from this parametrization.
This parametrization is famous among mathematicians, since it is the one welcoming the visitors at the Mathematisches Forschungsinstitut Oberwolfach
The Desargues Theorem
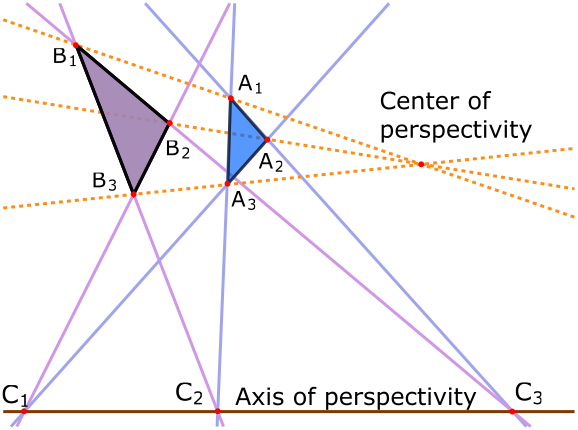
Start with two triangles in the real projective plane, with vertices say $A_1$, $A_2$, $A_3$ and $B_1, B_2, B_3$ in the projective plane. Consider now the following two questions:
- Question 1. Do the lines $(A_1B_1)$, $(A_2B_2)$ and $(A_3B_3)$ have a common intersection point?
- Question 2. Denote by $C_1$ – respectively $C_2$, $C_3$ — the intersection point of $(A_2A_3)$ and $(B_2B_3)$ — respectively $(A_3A_1)$ and $(B_3B_1)$, $(A_1A_2)$ and $(B_1B_2)$. Do the points $C_1$, $C_2$ and $C_3$ lie on the same line?
Desargues’ Theorem states that the answer to Question 1 is “Yes” if and only if the answer to Question 2 is “Yes” as well. The figure below represents a configuration of the Desargues theorem in the affine plane (i.e. when the two questions have a positive answer).
Desargues meets Boy
Since the Boy surface is a model of the projective plane, why not representing Desargues’ Theorem on it? The 3D printed object below displays a configuration of Desargues’ theorem on a Boy surface.
The triangles are represented in blue and purple. The lines $(A_1B_1)$, $(A_2B_2)$ and $(A_3B_3)$ are yellow. The points $C_1$, $C_2$ and $C_3$ lies on the brown line.
